Versione delle 12:27, 17 nov 2016

Indice

1 ATTENZIONE !!! - PAGINA IN ALLESTIMENTO

ATTENZIONE !!! - PAGINA IN ALLESTIMENTO

Vitoantonio Bevilacqua Strutture di controllo e Diagrammi di flusso vitoantonio.bevilacqua@poliba.it

Sommario. Il presente paragrafo si riferisce alle lezioni del I Modulo di Informatica : Fondamenti di Informatica per il nuovo corso di laurea triennale in Ingegneria dei Sistemi Medicali del Dipartimento di Ingegneria Elettrica e dell'Informazione del Politecnico di Bari.

Parole chiave: Algoritmo, Diagramma di flusso, Ricerca dicotomica.

Introduzione

Un algoritmo è una sequenza ordinata di passi elementari che consente di passare da dati in ingresso a dati in uscita; alcune delle proprietà fondamentali di un algoritmo sono:

eseguibilità: ogni parte, ogni diramazione dell’algoritmo deve essere percorribile;
non ambiguità: la scelta di un percorso rispetto ad un altro è legata ad una condizione (cioè da ogni punto del programma non devo poter andare dove voglio);
finitezza: l’algoritmo deve finire altrimenti si va in "loop".

Un diagramma di flusso è una rappresentazione simbolica di un algoritmo e ha lo scopo di esprimere il meccanismo di interazione con l’utenza e le operazioni da fare a partire dai dati inseriti. Le operazioni esplicitate in un algoritmo necessitano di essere eseguite sotto il controllo di un esecutore che le interpreta ed esegue nell’ordine logico di esecuzione. Poiché gli algoritmi che incontreremo dovranno essere eseguiti in maniera automatica, l’esecutore è l’elaboratore e quindi l’algoritmo dovrà essere tradotto in una sequenza di istruzioni scritte in un linguaggio che l’elaboratore è in grado di interpretare ed eseguire. Un linguaggio che ci consente di fare ciò è appunto il linguaggio MATLAB.

Struttura di un diagramma di flusso

Un qualsiasi diagramma di flusso è gestito da quattro schemi fondamentali che, opportunamente combinati attraverso delle frecce, rappresentano la sequenza logica e temporale dell’evoluzione dell’algoritmo. I quattro schemi hanno un ordine e un valore logico completamente diverso, e sono:

una "ellisse" che contiene al suo interno un label (etichetta) che può indicare l'"inizio" o la "fine" dell’algoritmo;
il "blocco delle assegnazioni", che contiene appunto un’assegnazione (p.e. i = 0); in particolare si assegna la parte destra del segno di = alla variabile a sinistra del segno; un’assegnazione del tipo i = 0 è un’assegnazione "di inizializzazione".
il "blocco di input/output": se di input, serve ad assegnare alla variabile contenuta nel blocco (ad es. N) un valore immesso dall’esterno; se di output, serve a stampare su video il valore della variabile contenuta nel blocco, precedentemente modificato dall'algoritmo.
il "blocco condizionale", che controlla se la condizione contenuta sia vera o no e restituisce l’esito vero o falso come output; quindi in un diagramma di flusso si trova sempre dopo altre operazioni di assegnazione o di input; si può presentare sotto due forme principali: ciclo con controllo in coda oppure decisione binaria V-F.

Ellisse di inizio e fine
Blocco delle assegnazioni
Blocchi di input/output
Blocco condizionale

Ciclo con controllo in coda

Controlla se la condizione espressa nel blocco sia vera o no. Nel primo caso viene rieseguito il blocco di operazioni comprese tra la punta della freccia di ritorno e il blocco condizionale; se la condizione risultasse falsa, allora si uscirebbe dal ciclo.

Rappresentazione di un ciclo con controllo in coda

Il seguente segmento di codice è la rappresentazione in codice matlab del ciclo con controllo in coda (è l'equivalente del ciclo do-while del linguaggio C). Come si può notare, è necessario utilizzare una variabile booleana affinché il costrutto presente in Matlab si comporti come un ciclo con controllo in coda.

%% Snippet di codice per il ciclo con controllo in coda

```
 
```
```
% Eseguo una serie di operazioni
```
```
 
```
```
% Utilizzo una variabile booleana
```
```
flag = true;
```
```
while flag == true
```
```
 
```
```
    % Eseguo diverse operazioni
```
```
 
```
```
    flag = condition
```
```
 
```
```
end
```

Decisione Binaria Vero-Falso

A seconda della veridicità o meno dell’espressione inserita si esegue il ramo del vero o del falso rispettivamente.

Rappresentazione di un blocco condizionale Vero - Falso

Il seguente segmento di codice è la rappresentazione in codice matlab del blocco di decisione binaria.

%% Snippet di codice per il blocco di decisione binaria if - else

```
% Eseguo una serie di operazioni
```
```
 
```
```
if condizione == true
```
```
 
```

    % Eseguo un determinato blocco di istruzioni

```
else
```
```
 
```

    % Eseguo un altro blocco di istruzioni

```
end
```

Esempi Applicativi

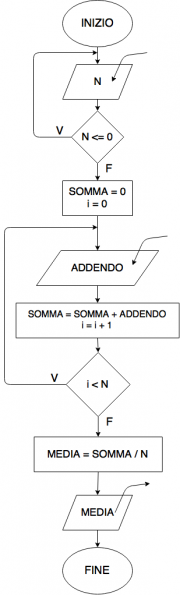
Media di una serie di numeri

Data una dimensione N, si vuole calcolare la media aritmetica di N numeri e mostrare il risultato a video.

Diagramma di flusso per il calcolo della media

```
%% Codice per il calcolo di N numeri
```
```
 
```

% Acquisisco da tastiera la dimensione dell'insieme di numeri

% controllando che sia un numero maggiore di 0

```
flag = true;
```
```
while flag == true
```
```
   N = input('');
```
```
   flag = N <= 0;
```
```
end
```
```
 
```

% Una volta acquisita la dimensione dell'insieme dei numeri, inizializzo le

% variabili utili al programma e passo ad acquisire i numeri

```
SOMMA = 0;
```
```
i = 0;
```
```
flag = true;
```
```
while flag == true
```
```
   ADDENDO = input('');
```
```
   SOMMA = SOMMA + ADDENDO;
```
```
   i = i+1;
```
```
   flag = i < N;
```
```
end
```
```
 
```
```
% Calcolo il valore di MEDIA
```
```
MEDIA = SOMMA / N;
```
```
 
```
```
% Stampo a video il valore di MEDIA
```
```
disp(MEDIA);
```
```
 
```
```
%% Riferimenti utili
```
```
%
```

% # https://www.mathworks.com/help/releases/R2016b/matlab/ref/input.html

% # https://www.mathworks.com/help/releases/R2016b/matlab/ref/while.html

% # https://www.mathworks.com/help/releases/R2016b/matlab/ref/disp.html

```
%
```

Somma dei numeri pari e prodotto dei numeri dispari

Dati N numeri, con N compreso tra 5 e 10, si vuole calcolare la somma dei numeri pari e il prodotto dei numeri dispari e mostrare tali valori a video

Diagramma di flusso per il calcolo della somma dei numeri pari e il prodotto dei numeri dispari

%% Codice per il calcolo della somma degli elementi pari e il prodotto di quelli dispari

```
 
```

% Acquisisco da tastiera la dimensione dell'insieme di numeri

% controllando che sia un numero compreso tra 5 e 10 (estremi inclusi)

```
flag = true;
```
```
while flag == true
```
```
    N = input('');
```
```
    flag = N < 5 || N > 10;
```
```
end
```
```
 
```

% Una volta acquisita la dimensione dell'insieme dei numeri, inizializzo le

% variabili utili al programma e passo ad acquisire i numeri

```
i = 0;
```
```
SOMMA = 0;
```
```
PROD = 1;
```
```
 
```
```
flag = true;
```
```
while flag == true
```
```
    operando = input('');
```

    % Controllo se l'operando è pari o dispari

```
    if mod(operando, 2) == 0
```

        % Caso relativo all'operando pari

```
       SOMMA = SOMMA + operando;
```
```
    else
```

         % Caso relativo all'operando dispari

```
        PROD = PROD * operando;
```
```
    end
```
```
 
```
```
    i = i+1;
```
```
    flag = i < N;
```
```
end
```
```
 
```
```
disp (SOMMA);
```
```
disp (PROD);
```
```
 
```
```
%% Riferimenti utili
```
```
%
```

% # https://www.mathworks.com/help/releases/R2016b/matlab/ref/while.html

% # https://www.mathworks.com/help/releases/R2016b/matlab/ref/input.html

% # https://it.mathworks.com/help/matlab/ref/logicaloperatorsshortcircuit.htm

% # https://www.mathworks.com/help/releases/R2016b/matlab/ref/mod.html

% # https://www.mathworks.com/help/releases/R2016b/matlab/ref/disp.html

```
%
```

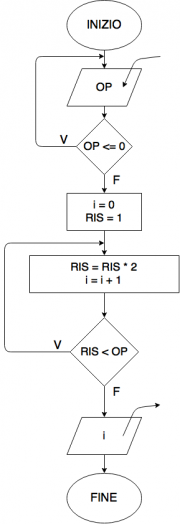
Logaritmo in base 2

Dato un numero maggiore di 0, si vuole calcolare il logaritmo in base 2 approssimato per eccesso di tale numero.

Diagramma di flusso per il calcolo del logaritmo in base 2 approssimato per eccesso

%% Codice per il calcolo dell'approssimazione per eccesso del logaritmo in base 2 di un numero

```
 
```

% Acquisisco da tastiera il numero di cui calcolare il logaritmo in base 2

% controllando che sia un numero maggiore di 0

```
flag = true;
```
```
while flag
```
```
    OP = input('');
```
```
    flag = OP <= 0;
```
```
end
```
```
 
```

% Una volta acquisito l'operando, inizializzo le variabili utili al programma

```
% e passo al calcolo del logaritmo
```
```
i = 0;
```
```
RIS = 1;
```
```
flag = true;
```
```
while flag == true
```
```
   RIS = RIS * 2;
```
```
   i = i+1;
```
```
   flag = RIS < OP;
```
```
end
```
```
 
```
```
% Mostro al video il risultato
```
```
disp(i)
```
```
 
```
```
%% Riferimenti utili
```
```
%
```

% # https://www.mathworks.com/help/releases/R2016b/matlab/ref/while.html

% # https://www.mathworks.com/help/releases/R2016b/matlab/ref/input.html

% # https://it.mathworks.com/help/matlab/ref/logicaloperatorsshortcircuit.htm

% # https://www.mathworks.com/help/releases/R2016b/matlab/ref/disp.html

```
%
```

Versione delle 12:23, 17 nov 2016 (visualizza sorgente) Profbevilacqua (Discussione \| contributi) ← Differenza precedente		Versione delle 12:27, 17 nov 2016 (visualizza sorgente) Profbevilacqua (Discussione \| contributi) Differenza successiva →
Riga 1:		Riga 1:
−	~~'''~~ATTENZIONE !!! - PAGINA IN ALLESTIMENTO~~'''~~	+	<h1 style="color: red;">ATTENZIONE !!! - PAGINA IN ALLESTIMENTO</h1>

	'''Vitoantonio Bevilacqua''' Strutture di controllo e Diagrammi di flusso [mailto:vitoantonio.bevilacqua@poliba.it vitoantonio.bevilacqua@poliba.it]		'''Vitoantonio Bevilacqua''' Strutture di controllo e Diagrammi di flusso [mailto:vitoantonio.bevilacqua@poliba.it vitoantonio.bevilacqua@poliba.it]

Diagrammi di flusso e Codice Matlab: differenze tra le versioni

Versione delle 12:27, 17 nov 2016

Indice

ATTENZIONE !!! - PAGINA IN ALLESTIMENTO

Introduzione

Struttura di un diagramma di flusso

Ciclo con controllo in coda

Decisione Binaria Vero-Falso

Esempi Applicativi

Media di una serie di numeri

Somma dei numeri pari e prodotto dei numeri dispari

Logaritmo in base 2

Menu di navigazione

Strumenti personali

Namespace

Varianti

Visite

Azioni

Ricerca

Navigazione

Strumenti